Chapter 1: BASIC AC THEORY

AC Phase

Things start to get complicated when we need to relate two or more AC voltages or currents that are out of step with each other. By "out of step", I mean that the two waveforms are not synchronized: that their peaks and zero points do not match up at the same points in time. The graph in figure below illustrates an example of this.

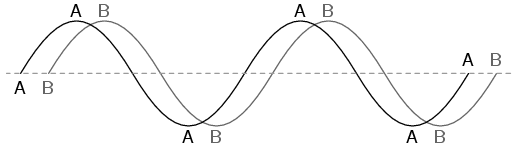
Out of phase waveforms

The two waves shown above (A versus B) are of the same amplitude and frequency, but they are out of step with each other. In technical terms, this is called a phase shift. Earlier we saw how we could plot a "sine wave" by calculating the trigonometric sine function for angles ranging from 0 to 360 degrees, a full circle. The starting point of a sine wave was zero amplitude at zero degrees, progressing to full positive amplitude at 90 degrees, zero at 180 degrees, full negative at 270 degrees, and back to the starting point of zero at 360 degrees. We can use this angle scale along the horizontal axis of our waveform plot to express just how far out of step one wave is with another: Figure below

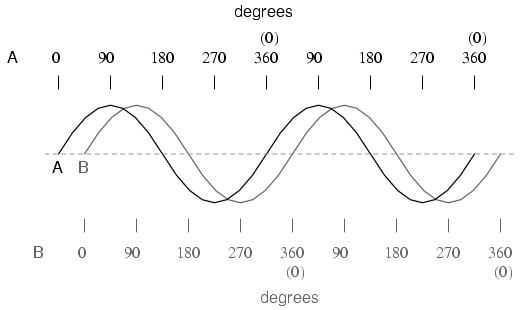
Wave A leads wave B by 45^o

The shift between these two waveforms is about 45 degrees, the "A" wave being ahead of the "B" wave. A sampling of different phase shifts is given in the following graphs to better illustrate this concept: Figure below

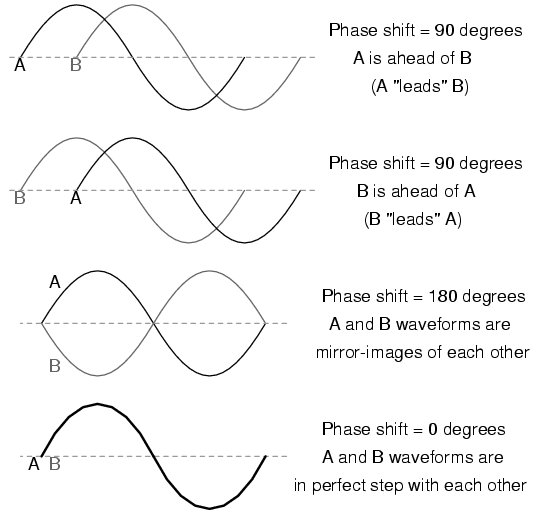
Examples of phase shifts.

Because the waveforms in the above examples are at the same frequency, they will be out of step by the same angular amount at every point in time. For this reason, we can express phase shift for two or more waveforms of the same frequency as a constant quantity for the entire wave, and not just an expression of shift between any two particular points along the waves. That is, it is safe to say something like, "voltage 'A' is 45 degrees out of phase with voltage 'B'". Whichever waveform is ahead in its evolution is said to be leading and the one behind is said to be lagging.

Phase shift, like voltage, is always a measurement relative between two things. There's really no such thing as a waveform with an absolute phase measurement because there's no known universal reference for phase. Typically in the analysis of AC circuits, the voltage waveform of the power supply is used as a reference for phase, that voltage stated as "xxx volts at 0 degrees". Any other AC voltage or current in that circuit will have its phase shift expressed in terms relative to that source voltage.

This is what makes AC circuit calculations more complicated than DC. When applying Ohm's Law and Kirchhoff's Laws, quantities of AC voltage and current must reflect phase shift as well as amplitude. Mathematical operations of addition, subtraction, multiplication, and division must operate on these quantities of phase shift as well as amplitude. Fortunately, there is a mathematical system of quantities called complex numbers ideally suited for this task of representing amplitude and phase.

Because the subject of complex numbers is so essential to the understanding of AC circuits, the next chapter will be devoted to that subject alone.

• REVIEW:
• Phase shift is where two or more waveforms are out of step with each other.
• The amount of phase shift between two waves can be expressed in terms of degrees, as defined by the degree units on the horizontal axis of the waveform graph used in plotting the trigonometric sine function.
• A leading waveform is defined as one waveform that is ahead of another in its evolution. A lagging waveform is one that is behind another. Example:

• 

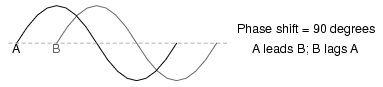
• Calculations for AC circuit analysis must take into consideration both amplitude and phase shift of voltage and current waveforms to be completely accurate. This requires the use of a mathematical system called complex numbers.