Chapter 10: POLYPHASE AC CIRCUITS

Harmonic Phase Sequences

In the last section, we saw how the 3rd harmonic and all of its integer multiples (collectively called triplen harmonics) generated by 120^o phase-shifted fundamental waveforms are actually in phase with each other. In a 60 Hz three-phase power system, where phases A, B, and C are 120^o apart, the third-harmonic multiples of those frequencies (180 Hz) fall perfectly into phase with each other. This can be thought of in graphical terms, (Figure below) and/or in mathematical terms:

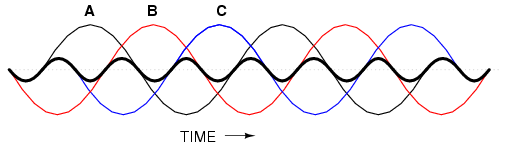
Harmonic currents of Phases A, B, C all coincide, that is, no rotation.

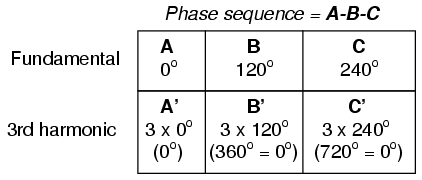
If we extend the mathematical table to include higher odd-numbered harmonics, we will notice an interesting pattern develop with regard to the rotation or sequence of the harmonic frequencies:

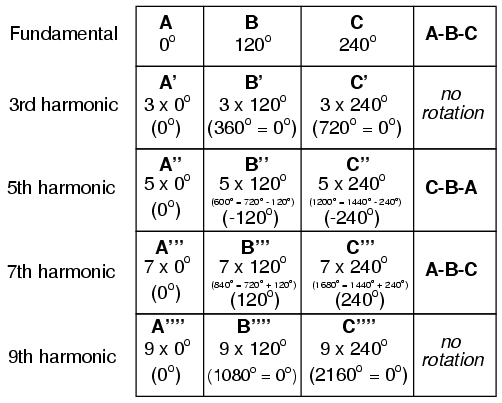
Harmonics such as the 7th, which “rotate” with the same sequence as the fundamental, are called positive sequence. Harmonics such as the 5th, which “rotate” in the opposite sequence as the fundamental, are called negative sequence. Triplen harmonics (3rd and 9th shown in this table) which don't “rotate” at all because they're in phase with each other, are called zero sequence.

This pattern of positive-zero-negative-positive continues indefinitely for all odd-numbered harmonics, lending itself to expression in a table like this:

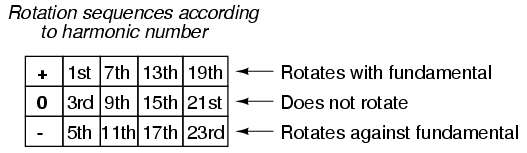
Sequence especially matters when we're dealing with AC motors, since the mechanical rotation of the rotor depends on the torque produced by the sequential “rotation” of the applied 3-phase power. Positive-sequence frequencies work to push the rotor in the proper direction, whereas negative-sequence frequencies actually work against the direction of the rotor's rotation. Zero-sequence frequencies neither contribute to nor detract from the rotor's torque. An excess of negative-sequence harmonics (5th, 11th, 17th, and/or 23rd) in the power supplied to a three-phase AC motor will result in a degradation of performance and possible overheating. Since the higher-order harmonics tend to be attenuated more by system inductances and magnetic core losses, and generally originate with less amplitude anyway, the primary harmonic of concern is the 5th, which is 300 Hz in 60 Hz power systems and 250 Hz in 50 Hz power systems.