Home > Textbooks > Lessons In Electric Circuits > Vol. II - AC > Power Factor > Power in Resistive and Reactive AC Circuits
Chapter 11: POWER FACTOR
Power in Resistive and Reactive AC Circuits
Consider a circuit for a single-phase AC power system, where a 120 volt, 60 Hz AC voltage source is delivering power to a resistive load: (Figure below)
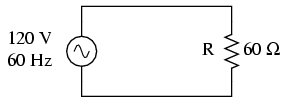
Ac source drives a purely resistive load.

In this example, the current to the load would be 2 amps, RMS. The power dissipated at the load would be 240 watts. Because this load is purely resistive (no reactance), the current is in phase with the voltage, and calculations look similar to that in an equivalent DC circuit. If we were to plot the voltage, current, and power waveforms for this circuit, it would look like Figure below.
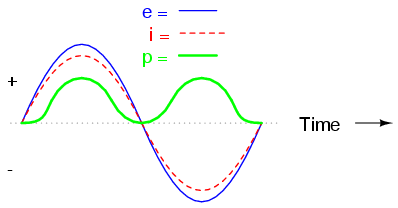
Current is in phase with voltage in a resistive circuit.
Note that the waveform for power is always positive, never negative for this resistive circuit. This means that power is always being dissipated by the resistive load, and never returned to the source as it is with reactive loads. If the source were a mechanical generator, it would take 240 watts worth of mechanical energy (about 1/3 horsepower) to turn the shaft.
Also note that the waveform for power is not at the same frequency as the voltage or current! Rather, its frequency is double that of either the voltage or current waveforms. This different frequency prohibits our expression of power in an AC circuit using the same complex (rectangular or polar) notation as used for voltage, current, and impedance, because this form of mathematical symbolism implies unchanging phase relationships. When frequencies are not the same, phase relationships constantly change.
As strange as it may seem, the best way to proceed with AC power calculations is to use scalar notation, and to handle any relevant phase relationships with trigonometry.
For comparison, let's consider a simple AC circuit with a purely reactive load in Figure below.

AC circuit with a purely reactive (inductive) load.

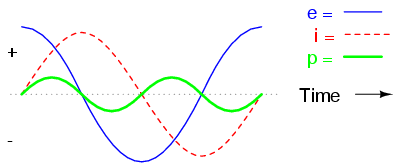
Power is not dissipated in a purely reactive load. Though it is alternately absorbed from and returned to the source.
Note that the power alternates equally between cycles of positive and negative. (Figure above) This means that power is being alternately absorbed from and returned to the source. If the source were a mechanical generator, it would take (practically) no net mechanical energy to turn the shaft, because no power would be used by the load. The generator shaft would be easy to spin, and the inductor would not become warm as a resistor would.
Now, let's consider an AC circuit with a load consisting of both inductance and resistance in Figure below.
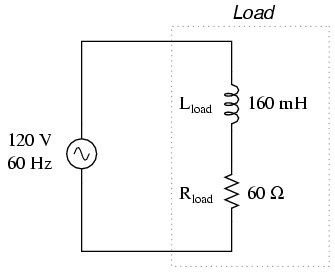
AC circuit with both reactance and resistance.
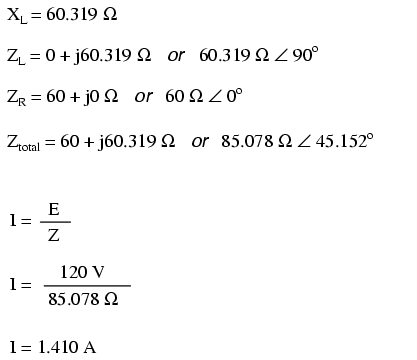
At a frequency of 60 Hz, the 160 millihenrys of inductance gives us 60.319 Ω of inductive reactance. This reactance combines with the 60 Ω of resistance to form a total load impedance of 60 + j60.319 Ω, or 85.078 Ω ∠ 45.152o. If we're not concerned with phase angles (which we're not at this point), we may calculate current in the circuit by taking the polar magnitude of the voltage source (120 volts) and dividing it by the polar magnitude of the impedance (85.078 Ω). With a power supply voltage of 120 volts RMS, our load current is 1.410 amps. This is the figure an RMS ammeter would indicate if connected in series with the resistor and inductor.
We already know that reactive components dissipate zero power, as they equally absorb power from, and return power to, the rest of the circuit. Therefore, any inductive reactance in this load will likewise dissipate zero power. The only thing left to dissipate power here is the resistive portion of the load impedance. If we look at the waveform plot of voltage, current, and total power for this circuit, we see how this combination works in Figure below.
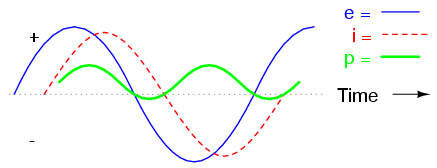
A combined resistive/reactive circuit dissipates more power than it returns to the source. The reactance dissipates no power; though, the resistor does.
As with any reactive circuit, the power alternates between positive and negative instantaneous values over time. In a purely reactive circuit that alternation between positive and negative power is equally divided, resulting in a net power dissipation of zero. However, in circuits with mixed resistance and reactance like this one, the power waveform will still alternate between positive and negative, but the amount of positive power will exceed the amount of negative power. In other words, the combined inductive/resistive load will consume more power than it returns back to the source.
Looking at the waveform plot for power, it should be evident that the wave spends more time on the positive side of the center line than on the negative, indicating that there is more power absorbed by the load than there is returned to the circuit. What little returning of power that occurs is due to the reactance; the imbalance of positive versus negative power is due to the resistance as it dissipates energy outside of the circuit (usually in the form of heat). If the source were a mechanical generator, the amount of mechanical energy needed to turn the shaft would be the amount of power averaged between the positive and negative power cycles.
Mathematically representing power in an AC circuit is a challenge, because the power wave isn't at the same frequency as voltage or current. Furthermore, the phase angle for power means something quite different from the phase angle for either voltage or current. Whereas the angle for voltage or current represents a relative shift in timing between two waves, the phase angle for power represents a ratio between power dissipated and power returned. Because of this way in which AC power differs from AC voltage or current, it is actually easier to arrive at figures for power by calculating with scalar quantities of voltage, current, resistance, and reactance than it is to try to derive it from vector, or complex quantities of voltage, current, and impedance that we've worked with so far.
- REVIEW:
- In a purely resistive circuit, all circuit power is dissipated by the resistor(s). Voltage and current are in phase with each other.
- In a purely reactive circuit, no circuit power is dissipated by the load(s). Rather, power is alternately absorbed from and returned to the AC source. Voltage and current are 90o out of phase with each other.
- In a circuit consisting of resistance and reactance mixed, there will be more power dissipated by the load(s) than returned, but some power will definitely be dissipated and some will merely be absorbed and returned. Voltage and current in such a circuit will be out of phase by a value somewhere between 0o and 90o.
Related Content:
Video lecture: What is Power Factor?






