Home > Textbooks > Lessons In Electric Circuits > Vol. II - AC > Complex Numbers > Introduction
Chapter 2: COMPLEX NUMBERS
Introduction
If I needed to describe the distance between two cities, I could provide an answer consisting of a single number in miles, kilometers, or some other unit of linear measurement. However, if I were to describe how to travel from one city to another, I would have to provide more information than just the distance between those two cities; I would also have to provide information about the direction to travel, as well.
The kind of information that expresses a single dimension, such as linear distance, is called a scalar quantity in mathematics. Scalar numbers are the kind of numbers you've used in most all of your mathematical applications so far. The voltage produced by a battery, for example, is a scalar quantity. So is the resistance of a piece of wire (ohms), or the current through it (amps).
However, when we begin to analyze alternating current circuits, we find that quantities of voltage, current, and even resistance (called impedance in AC) are not the familiar one-dimensional quantities we're used to measuring in DC circuits. Rather, these quantities, because they're dynamic (alternating in direction and amplitude), possess other dimensions that must be taken into account. Frequency and phase shift are two of these dimensions that come into play. Even with relatively simple AC circuits, where we're only dealing with a single frequency, we still have the dimension of phase shift to contend with in addition to the amplitude.
In order to successfully analyze AC circuits, we need to work with mathematical objects and techniques capable of representing these multi-dimensional quantities. Here is where we need to abandon scalar numbers for something better suited: complex numbers. Just like the example of giving directions from one city to another, AC quantities in a single-frequency circuit have both amplitude (analogy: distance) and phase shift (analogy: direction). A complex number is a single mathematical quantity able to express these two dimensions of amplitude and phase shift at once.
Complex numbers are easier to grasp when they're represented graphically. If I draw a line with a certain length (magnitude) and angle (direction), I have a graphic representation of a complex number which is commonly known in physics as a vector: (Figure below)

A vector has both magnitude and direction.
Like distances and directions on a map, there must be some common frame of reference for angle figures to have any meaning. In this case, directly right is considered to be 0o, and angles are counted in a positive direction going counter-clockwise: (Figure below)
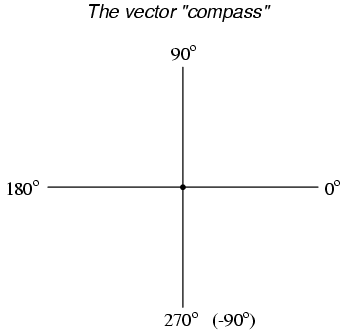
The vector compass
The idea of representing a number in graphical form is nothing new. We all learned this in grade school with the "number line:" (Figure below)

Number line.
We even learned how addition and subtraction works by seeing how lengths (magnitudes) stacked up to give a final answer: (Figure below)
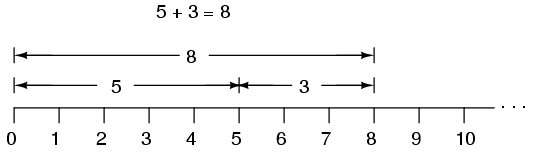
Addition on a "number line".
Later, we learned that there were ways to designate the values between the whole numbers marked on the line. These were fractional or decimal quantities: (Figure below)
Locating a fraction on the "number line"
Later yet we learned that the number line could extend to the left of zero as well: (Figure below)
"Number line" shows both positive and negative numbers.
These fields of numbers (whole, integer, rational, irrational, real, etc.) learned in grade school share a common trait: they're all one-dimensional. The straightness of the number line illustrates this graphically. You can move up or down the number line, but all "motion" along that line is restricted to a single axis (horizontal). One-dimensional, scalar numbers are perfectly adequate for counting beads, representing weight, or measuring DC battery voltage, but they fall short of being able to represent something more complex like the distance and direction between two cities, or the amplitude and phase of an AC waveform. To represent these kinds of quantities, we need multidimensional representations. In other words, we need a number line that can point in different directions, and that's exactly what a vector is.
- REVIEW:
- A scalar number is the type of mathematical object that people are used to using in everyday life: a one-dimensional quantity like temperature, length, weight, etc.
- A complex number is a mathematical quantity representing two dimensions of magnitude and direction.
- A vector is a graphical representation of a complex number. It looks like an arrow, with a starting point, a tip, a definite length, and a definite direction. Sometimes the word phasor is used in electrical applications where the angle of the vector represents phase shift between waveforms.
Related Content:
Video lecture: The Complex Numbers






