Chapter 2: SOLID-STATE DEVICE THEORY

Band Theory of Solids

Quantum physics describes the states of electrons in an atom according to the four-fold scheme of quantum numbers. The quantum numbers describe the allowable states electrons may assume in an atom. To use the analogy of an amphitheater, quantum numbers describe how many rows and seats are available. Individual electrons may be described by the combination of quantum numbers, like a spectator in an amphitheater assigned to a particular row and seat.

Like spectators in an amphitheater moving between seats and rows, electrons may change their statuses, given the presence of available spaces for them to fit, and available energy. Since shell level is closely related to the amount of energy that an electron possesses, “leaps” between shell (and even subshell) levels requires transfers of energy. If an electron is to move into a higher-order shell, it requires that additional energy be given to the electron from an external source. Using the amphitheater analogy, it takes an increase in energy for a person to move into a higher row of seats, because that person must climb to a greater height against the force of gravity. Conversely, an electron “leaping” into a lower shell gives up some of its energy, like a person jumping down into a lower row of seats, the expended energy manifesting as heat and sound.

Not all “leaps” are equal. Leaps between different shells require a substantial exchange of energy, but leaps between subshells or between orbitals require lesser exchanges.

When atoms combine to form substances, the outermost shells, subshells, and orbitals merge, providing a greater number of available energy levels for electrons to assume. When large numbers of atoms are close to each other, these available energy levels form a nearly continuous band wherein electrons may move as illustrated in Figure below

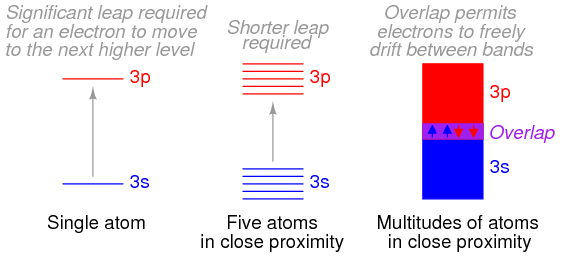
Electron band overlap in metallic elements.

It is the width of these bands and their proximity to existing electrons that determines how mobile those electrons will be when exposed to an electric field. In metallic substances, empty bands overlap with bands containing electrons, meaning that electrons of a single atom may move to what would normally be a higher-level state with little or no additional energy imparted. Thus, the outer electrons are said to be “free”, and ready to move at the beckoning of an electric field.

Band overlap will not occur in all substances, no matter how many atoms are close to each other. In some substances, a substantial gap remains between the highest band containing electrons (the so-called valence band) and the next band, which is empty (the so-called conduction band). See Figure below. As a result, valence electrons are “bound” to their constituent atoms and cannot become mobile within the substance without a significant amount of imparted energy. These substances are electrical insulators.

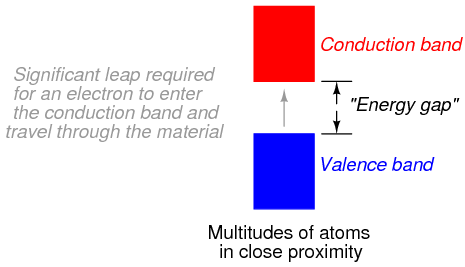
Electron band separation in insulating substances.

Materials that fall within the category of semiconductors have a narrow gap between the valence and conduction bands. Thus, the amount of energy required to motivate a valence electron into the conduction band where it becomes mobile is quite modest. (Figure below)

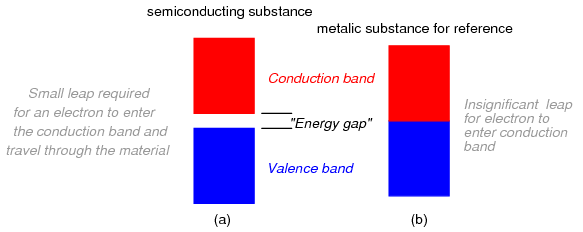
Electron band separation in semiconducting substances, (a) multitudes of semiconducting close atoms still results in a significant band gap, (b) multitudes of close metal atoms for reference.

At low temperatures, little thermal energy is available to push valence electrons across this gap, and the semiconducting material acts more as an insulator. At higher temperatures, though, the ambient thermal energy becomes enough to force electrons across the gap, and the material will increase conduction of electricity.

It is difficult to predict the conductive properties of a substance by examining the electron configurations of its constituent atoms. Although the best metallic conductors of electricity (silver, copper, and gold) all have outer s subshells with a single electron, the relationship between conductivity and valence electron count is not necessarily consistent:

The electron band configurations produced by compounds of different elements defies easy association with the electron configurations of its constituent elements.

• REVIEW:
• Energy is required to remove an electron from the valence band to a higher unoccupied band, a conduction band. More energy is required to move between shells, less between subshells.
• Since the valence and conduction bands overlap in metals, little energy removes an electron. Metals are excellent conductors.
• The large gap between the valence and conduction bands of an insulator requires high energy to remove an electron. Thus, insulators do not conduct.
• Semiconductors have a small non-overlapping gap between the valence and conduction bands. Pure semiconductors are neither good insulators nor conductors. Semiconductors are semi-conductive.