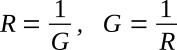Resistors

Introduction

Resistors are components manufactured to possess specific values of resistance.

Electrical resistance

It is known that the directed movement of electrons constitutes a current flow. It is also known that the electrons do not move freely through a conductor’s crystalline structure. Some materials offer little opposition to current flow, while others greatly oppose current flow. This opposition to current flow is known as resistance (R), and the unit of measure is the ohm. The standard of measure for one ohm is the resistance provided at zero degrees Celsius by a column of mercury having a cross-sectional area of one square millimeter and a length of 106.3 centimeters. A conductor has one ohm of resistance when an applied potential of one volt produces a current of one ampere. The symbol used to represent the ohm is the Greek letter omega (Ω).

Resistance, although an electrical property, is determined by the physical structure of a material. The resistance of a material is governed by many of the same factors that control current flow. Therefore, in a subsequent discussion, the factors that affect current flow will be used to assist in the explanation of the factors affecting resistance.

Factors That Affect Resistance

The magnitude of resistance is determined in part by the "number of free electrons" available within the material. Since a decrease in the number of free electrons will decrease the current flow, it can be said that the opposition to current flow (resistance) is greater in a material with fewer free electrons. Thus, the resistance of a material is determined by the number of free electrons available in a material.

A knowledge of the conditions that limit current flow and, therefore, affect resistance can now be used to consider how the type of material, physical dimensions, and temperature will affect the resistance of a conductor.

Type of Material

Depending upon their atomic structure, different materials will have different quantities of free electrons. Therefore, the various conductors used in electrical applications have different values of resistance.

Consider a simple metallic substance. Most metals are crystalline in structure and consist of atoms that are tightly bound in the lattice network. The atoms of such elements are so close together that the electrons in the outer shell of the atom are associated with one atom as much as with its neighbor. (See the figure below, view A). As a result, the force of attachment of an outer electron with an individual atom is practically zero. Depending on the metal, at least one electron, sometimes two, and in a few cases, three electrons per atom exist in this state. In such a case, a relatively small amount of additional electron energy would free the outer electrons from the attraction of the nucleus. At normal room temperature materials of this type have many free electrons and are good conductors. Good conductors will have a low resistance.

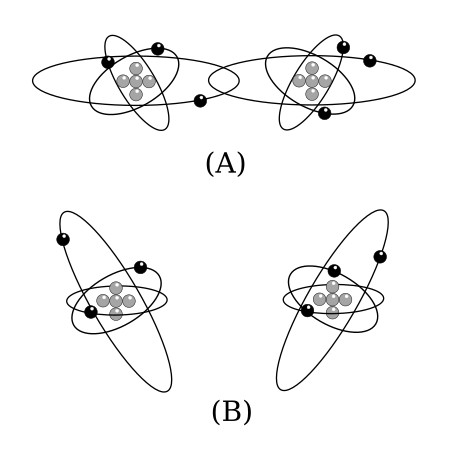
If the atoms of a material are farther apart, as illustrated in the figure above, view B, the electrons in the outer shells will not be equally attached to several atoms as they orbit the nucleus. They will be attracted by the nucleus of the parent atom only. Therefore, a greater amount of energy is required to free any of these electrons. Materials of this type are poor conductors and therefore have a high resistance.

Silver, gold, and aluminum are good conductors. Therefore, materials composed of their atoms would have a low resistance.

The element copper is the conductor most widely used throughout electrical applications. Silver has a lower resistance than copper but its cost limits usage to circuits where a high conductivity is demanded.

Aluminum, which is considerably lighter than copper, is used as a conductor when weight is a major factor.

Effect of Cross-Sectional Area

Cross-sectional area greatly affects the magnitude of resistance. If the cross-sectional area of a conductor is increased, a greater quantity of electrons are available for movement through the conductor. Therefore, a larger current will flow for a given amount of applied voltage. An increase in current indicates that when the cross-sectional area of a conductor is increased, the resistance must have decreased. Thus, the resistance of a conductor is inversely proportional to its cross-sectional area.

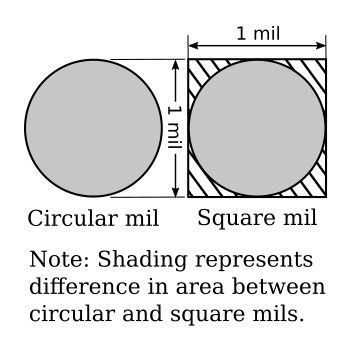
The diameter of conductors used in electronics is often only a fraction of an inch, therefore, the diameter is expressed in mils (thousandths of an inch). It is also standard practice to assign the unit circular mil to the cross-sectional area of the conductor. The circular mil is found by squaring the diameter when the diameter is expressed in mils. Thus, if the diameter is 35 mils (0.035 inch), the circular mil area is equal to 35² or 1225 circular mils. A comparison between a square mil and a circular mil is illustrated in the figure below.

Effect of Conductor Length

The length of a conductor is also a factor which determines the resistance of a conductor. If the length of a conductor is increased, the amount of energy given up increases. As free electrons move from atom to atom some energy is given off as heat. The longer a conductor is, the more energy is lost to heat. The additional energy loss subtracts from the energy being transferred through the conductor, resulting in a decrease in current flow for a given applied voltage. A decrease in current flow indicates an increase in resistance, since voltage was held constant. Therefore, if the length of a conductor is increased, the resistance increases. The resistance of a conductor is directly proportional to its length.

Effect of Temperature

Temperature changes affect the resistance of materials in different ways. In some materials an increase in temperature causes an increase in resistance, whereas in others, an increase in temperature causes a decrease in resistance. The amount of change of resistance per unit change in temperature is known as the temperature coefficient. If for an increase in temperature the resistance of a material increases, it is said to have a positive temperature coefficient. A material whose resistance decreases with an increase in temperature has a negative temperature coefficient. Most conductors used in electronic applications have a positive temperature coefficient. However, carbon, a frequently used material, is a substance having a negative temperature coefficient. Several materials, such as the alloys constantan and manganin, are considered to have a zero temperature coefficient because their resistance remains relatively constant for changes in temperature.

Conductance

Electricity is a study that is frequently explained in terms of opposites. The term that is the opposite of resistance is conductance. Conductance is the ability of a material to pass electrons. The factors that affect the magnitude of resistance are exactly the same for conductance, but they affect conductance in the opposite manner. Therefore, conductance is directly proportional to area, and inversely proportional to the length of the material. The temperature of the material is definitely a factor, but assuming a constant temperature, the conductance of a material can be calculated.

The unit of conductance is the siemens (S). The relationship that exists between resistance (R) and conductance (G) is a reciprocal one. A reciprocal of a number is one divided by that number. In terms of resistance and conductance