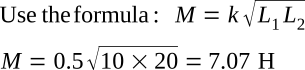Inductors

Mutual Inductance

Whenever two coils are located so that the flux from one coil links with the turns of the other coil, a change of flux in one coil causes an EMF to be induced in the other coil. This allows the energy from one coil to be transferred or coupled to the other coil. The two coils are said to be coupled or linked by the property of mutual inductance (M). The amount of mutual inductance depends on the relative positions of the two coils. This is shown in the figure below. If the coils are separated a considerable distance, the amount of flux common to both coils is small and the mutual inductance is low. Conversely, if the coils are close together so that nearly all the flux of one coil links the turns of the other, the mutual inductance is high. The mutual inductance can be increased greatly by mounting the coils on a common iron core.

The effect of position of coils on mutual inductance (M).

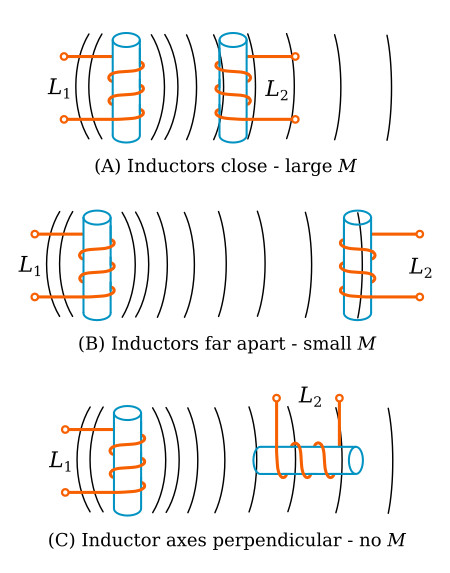
Two coils are placed close together as shown in the figure below. Coil 1 is connected to a battery through switch S, and coil 2 is connected to an ammeter (A). When switch S is closed as in view A, the current that flows in coil 1 sets up a magnetic field that links with coil 2, causing an induced voltage in coil 2 and a momentary deflection of the ammeter. When the current in coil 1 reaches a steady value, the ammeter returns to zero. If switch S is now opened as in view B, the ammeter (A) deflects momentarily in the opposite direction, indicating a momentary flow of current in the opposite direction in coil 2. This current in coil 2 is produced by the collapsing magnetic field of coil 1.

Mutual inductance.

Factors Affecting Mutual Inductance

The mutual inductance of two adjacent coils is dependent upon the physical dimensions of the two coils, the number of turns in each coil, the distance between the two coils, the relative positions of the axes of the two coils, and the permeability of the cores.

The coefficient of coupling between two coils is equal to the ratio of the flux cutting one coil to the flux originated in the other coil. If the two coils are so positioned with respect to each other so that all of the flux of one coil cuts all of the turns of the other, the coils are said to have a unity coefficient of coupling. It is never exactly equal to unity (1), but it approaches this value in certain types of coupling devices. If all of the flux produced by one coil cuts only half the turns of the other coil, the coefficient of coupling is 0.5. The coefficient of coupling is designated by the letter k.

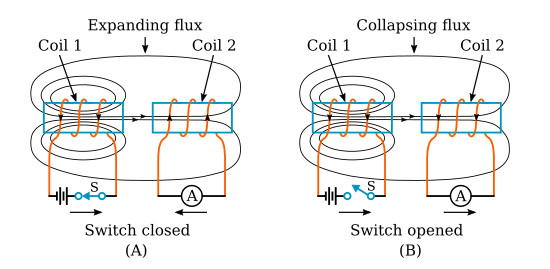
The mutual inductance between two coils, L₁ and L₂, is expressed in terms of the inductance of each coil and the coefficient of coupling k. As a formula

where
M is mutual inductance in henrys
k is coefficient of coupling
L₁, L₂ are inductances of coils in henrys

Example problem:

One 10-H coil and one 20-H coil are connected in series and are physically close enough to each other so that their coefficient of coupling is 0.5. What is the mutual inductance between the coils?