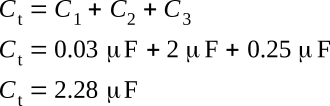Capacitors

Capacitors in Series and Parallel

Capacitors may be connected in series or in parallel to obtain a resultant value which may be either the sum of the individual values (in parallel) or a value less than that of the smallest capacitance (in series).

Capacitors in Series

A circuit consisting of a number of capacitors in series is similar in some respects to one containing several resistors in series. In a series capacitive circuit the same displacement current flows through each part of the circuit and the applied voltage will divide across the individual capacitors. The figure below shows a circuit containing a source and three series capacitors.

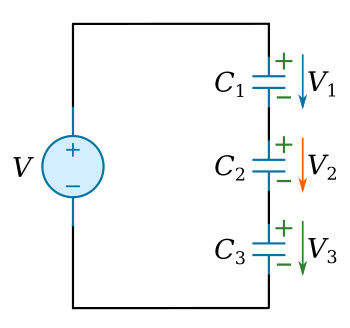
The sum of the capacitor voltages must equal the source voltage (Kirchhoff's voltage law)

The charges on all capacitors must be the same, since the capacitors are connected in series and any charge movement in one part of the circuit must take place in all parts of the series circuit. Solving the equation C=Q/V for voltage in terms of capacitance and charge (V=Q/C), the following results are obtained for each of the series capacitors and the total capacitance (C_t)

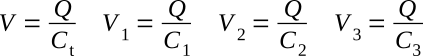
Substituting these results into the above Kirchhoff's voltage law equation

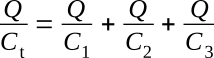
Dividing both sides of the above equation by the common factor Q

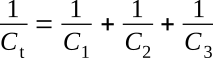
Taking the reciprocal of both sides and assuming any number of capacitors

This equation is the general equation used to compute the total capacitance of capacitors connected in series. Notice the similarity between this equation and the one used to find equivalent resistance of parallel resistors. If the circuit contains only two capacitors the product over the sum formula can be used

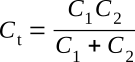
It should be evident from the above formulas that the total capacitance of capacitors in series is less than the capacitance of any of the individual capacitors.

Example:
Determine the total capacitance of a series circuit containing three capacitors whose values are 10 nF, 0.25 µF, and 50 nF, respectively.

Solution:

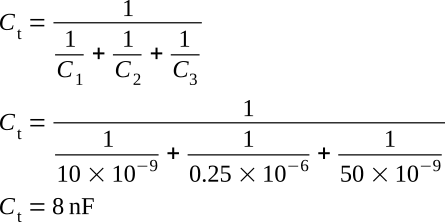
The total capacitance of 8 nF is slightly smaller than the smallest capacitor (10 nF).

Capacitors in Parallel

When capacitors are connected in parallel (see the figure below), one plate of each capacitor is connected directly to one terminal of the source, while the other plate of each capacitor is connected to the other terminal of the source. In the figure below, all the negative plates of the capacitors are connected together, and all the positive plates are connected together. The total (equivalent) capacitance C_t, therefore, appears as a capacitance with a plate area equal to the sum of all the individual plate areas. As previously mentioned, capacitance is a direct function of plate area. Connecting capacitors in parallel effectively increases plate area and thereby increases total capacitance.

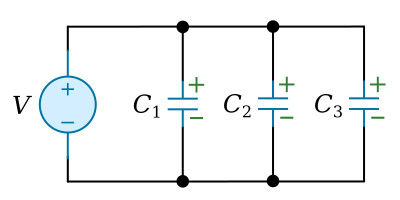
The total capacitance can be calculated mathematically. By applying the equation C=Q/V to each capacitor and to the total capacitance

The total charge Q_t is the sum of the charges on each capacitor

From the equation C=Q/V, it follows that Q=CV, and if the charge is written in this form and substituted into the above equation, this equation results

Dividing both sides of the above equation by the common factor V and assuming any number of capacitors

This equation states mathematically that the total capacitance of a number of capacitors in parallel is the sum of the individual capacitances.

Example:
Determine the total capacitance in a parallel capacitive circuit containing three capacitors whose values are 30 nF, 2 µF, and 0.25 µF, respectively.

Solution: