DC Network Analysis

Norton's Theorem

Norton's theorem provides a second method of reducing complex circuitry to a simple equivalent circuit.

Norton's theorem is especially useful in analyzing circuits where only one particular resistor in the circuit (called the load) is subject to change. Example:

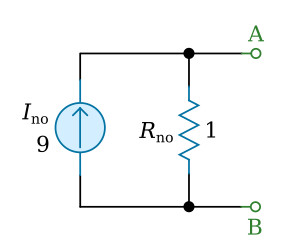
Norton's theorem states: Any linear electrical circuit can be replaced at terminals A and B by a simple parallel circuit consisting of an equivalent current source I_no and an equivalent resistance R_no.

The equivalent parallel circuit will provide the same current through a load as would the original circuit. The equivalent current I_no is the current that would flow through a short circuit between the two terminals (A and B) being considered in the original network. The equivalent resistance R_no is the resistance "seen" between the two terminals being considered in the original network when all voltage sources of the original circuit are replaced by a short circuit (wire) and all current sources are replaced by an open circuit (break).

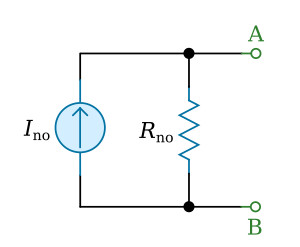
The figure below shows the application of Norton's theorem to a simple network. When Norton's theorem is applied, the current through R_L of the figure below (view A) is the same as the current in R_L of the figure below (view D).

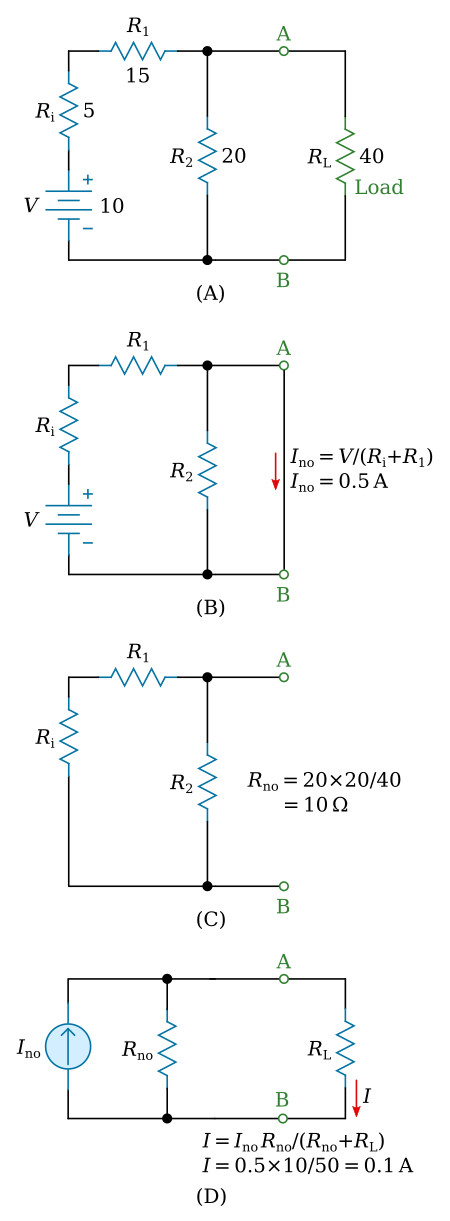
In Norton's theorem, as in Thevenin's theorem, the equivalency is established for the chosen load terminals. Therefore, the equivalency applies only at the load.

Application of Norton's theorem is further illustrated in the following examples.

Example 1:
Find the Norton-equivalent circuit of the circuit shown in the figure below.

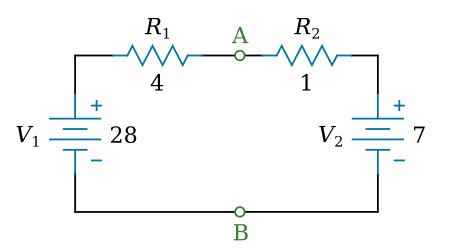
Solution:

Calculating the equivalent current I_no

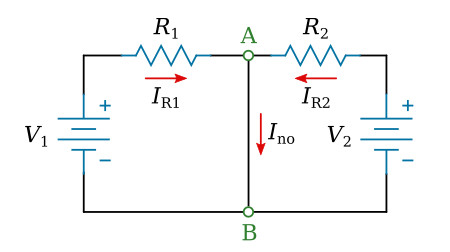
Place a wire (short) between the points A and B (figure above), and use Ohm's law to calculate the currents through resistors R₁ and R₂:

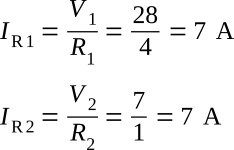
The current through the short between the points A and B is the sum of the currents I_R1 and I_R2:

Calculating the equivalent resistance R_no

Replace the voltage sources V₁ and V₂ with a wire:

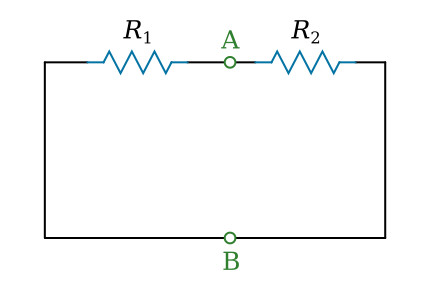
The resistance between the points A and B is equal to R₁ and R₂ in parallel: 0.8 Ω. This is our equivalent resistance R_no in the equivalent circuit:

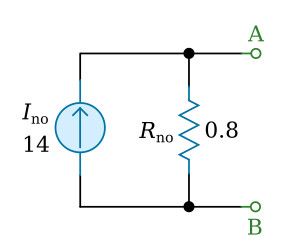
Example 2:
Find the Norton-equivalent circuit of the circuit shown in the figure below.

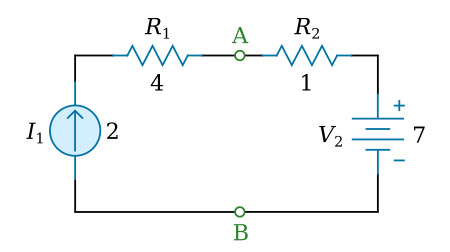
Solution:

Calculating the equivalent current I_no

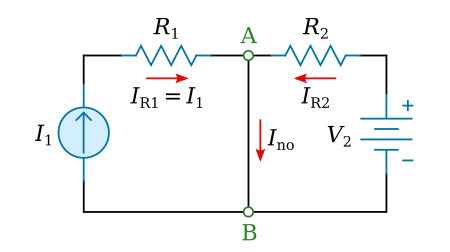
Place a wire (short) between the points A and B (figure above), and use Ohm's law to calculate the currents through resistor R₂:

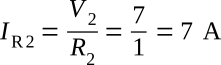
The current through the short between the points A and B is the sum of the currents I_R1 and I_R2:

Calculating the equivalent resistance R_no

Replace the current source I₁ with a break and the voltage source V₂ with a wire:

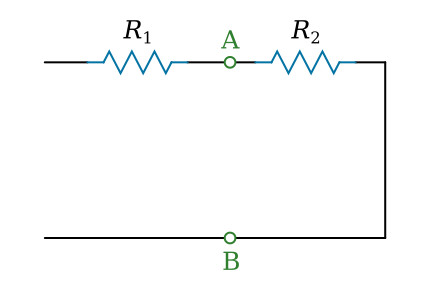
The resistance between the points A and B is equal to R₂: 1 Ω. This is our equivalent resistance R_no in the equivalent circuit: