Operational Amplifiers

Closed-Loop Operation of an Opamp

Operational amplifiers can have either a closed-loop operation or an open-loop operation. The operation (closed-loop or open-loop) is determined by whether or not feedback is used. Without feedback the operational amplifier has an open-loop operation. This open-loop operation is practical only when the operational amplifier is used as a comparator (a circuit which compares two input signals or compares an input signal to some fixed level of voltage). As an amplifier, the open-loop operation is not practical because the very high gain of the operational amplifier creates poor stability. (Noise and other unwanted signals are amplified so much in open-loop operation that the operational amplifier is usually not used in this way.) Therefore, most operational amplifiers are used with feedback (closed-loop operation).

Operational amplifiers are used with degenerative (or negative) feedback which reduces the gain of the operational amplifier but greatly increases the stability of the circuit. In the closed-loop configuration, the output signal is applied back to one of the input terminals. This feedback is always degenerative (negative). In other words, the feedback signal always opposes the effects of the original input signal. One result of degenerative feedback is that the inverting and noninverting inputs to the operational amplifier will be kept at the same potential.

Closed-loop circuits can be of the inverting configuration or noninverting configuration. Since the inverting configuration is used more often than the noninverting configuration, the inverting configuration will be shown first.

Inverting Amplifier Configuration

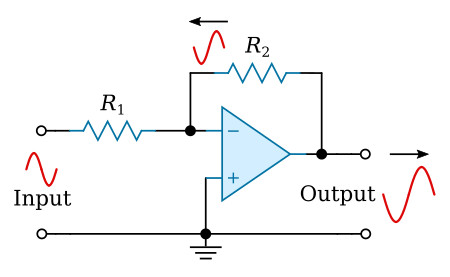
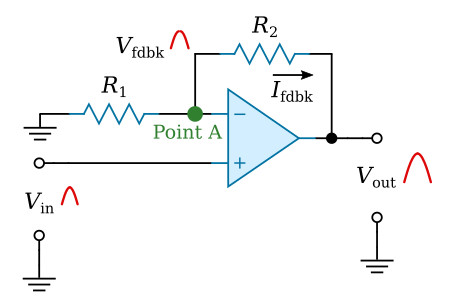
The figure above shows an operational amplifier in a closed-loop, inverting amplifier configuration. Resistor R₂ is used to feed part of the output signal back to the input of the operational amplifier.

At this point it is important to keep in mind the difference between the entire circuit (or operational circuit) and the operational amplifier. The operational amplifier is represented by the triangle-like symbol while the operational circuit includes the resistors and any other components as well as the operational amplifier. In other words, the input to the circuit is shown in the figure above, but the signal at the inverting input of the operational amplifier is determined by the feedback signal as well as by the circuit input signal.

As you can see in the figure above, the output signal is 180 degrees out of phase with the input signal. The feedback signal is a portion of the output signal and, therefore, also 180 degrees out of phase with the input signal. Whenever the input signal goes positive, the output signal and the feedback signal go negative. The result of this is that the inverting input to the operational amplifier is always very close to 0 volts with this configuration. In fact, with the noninverting input grounded, the voltage at the inverting input to the operational amplifier is so small compared to other voltages in the circuit that it is considered to be virtual ground. (Remember, in a closed-loop operation the inverting and noninverting inputs are at the same potential.) Virtual ground is a point in a circuit which is at ground potential (0 volts) but is not connected to ground.

Because the inverting input is at 0 volts, there will be no current (for all practical purposes) flowing into the operational amplifier from the connection point of R₁ and R₂. Given these conditions, the characteristics of this circuit are determined almost entirely by the values of R₁ and R₂. The figure below should help show how the values of R₁ and R₂ determine the circuit characteristics.

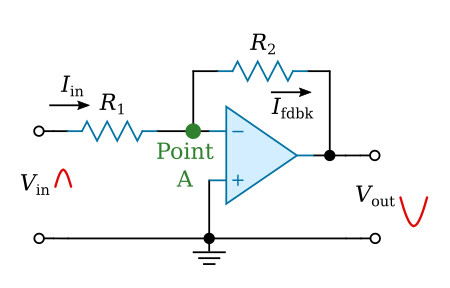
Note: It should be stressed at this point that for purpose of explanation the operational amplifier is a theoretically perfect amplifier. In actual practice we are dealing with less than perfect. In the practical operational amplifier there will be a slight input current with a resultant power loss. This small signal can be measured at the theoretical point of virtual ground. This does not indicate faulty operation.

The input signal causes current to flow through R₁. (Only the positive half cycle of the input signal is shown and will be discussed.) Since the voltage at the inverting input of the operational amplifier is at 0 volts, the input current (I_in) is computed by:

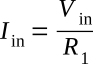
The output signal (which is opposite in phase to the input signal) causes a feedback current (I_fdbk) to flow through R₂. The left-hand side of R₂ is at 0 volts (point A) and the right-hand side is at V_out. Therefore, the feedback current is computed by:

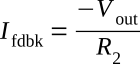
(The minus sign indicates that V_out is 180 degrees out of phase with V_in and should not be confused with output polarity.)

Since no current flows into or out of the inverting input of the operational amplifier, any current reaching point A from R₁ must flow out of point A through R₂. Therefore, the input current (I_in) and the feedback current (I_fdbk) must be equal. Now we can develop a mathematical relationship between the input and output signals and R₁ and R₂. Mathematically:

By substitution:

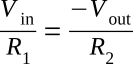
If you multiply both sides of the equation by R₁:

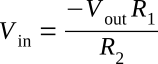
If you divide both sides of the equation by V_out:

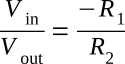
By inverting both sides of the equation:

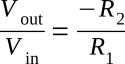
You should recall that the voltage gain of a stage is defined as the output voltage divided by the input voltage:

Therefore, the voltage gain of the inverting configuration of the operational amplifier is expressed by the equation:

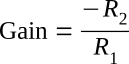
(As stated earlier, the minus sign indicates that the output signal is 180 degrees out of phase with the input signal.)

Noninverting Amplifier Configuration

The figure above shows a noninverting configuration using an operational amplifier. The input signal (V_in) is applied directly to the noninverting (+) input of the operational amplifier. Feedback is provided by coupling part of the output signal (V_out) back to the inverting (-) input of the operational amplifier. R₁ and R₂ act as voltage divider that allows only a part of the output signal to be applied as feedback (V_fdbk).

Notice that the input signal, output signal, and feedback signal are all in phase. (Only the positive alternation of the signal is shown.) It may appear as if the feedback is regenerative (positive) because the feedback and input signals are in phase. The feedback is, in reality, degenerative (negative) because the input signal is applied to the noninverting input and the feedback signal is applied to the inverting input. (Remember, that the operational amplifier will react to the difference between the two inputs.)

Just as in the inverting configuration, the feedback signal is equal to the input signal (for all practical purposes). This time, however, the feedback signal is in phase with the input signal. Therefore:

Given this condition, you can calculate the gain of the stage in terms of the resistors (R₁ and R₂).

The gain of the stage is defined as:

Since:

Then:

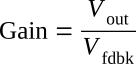
The feedback signal (V_fdbk) can be shown in terms of the output signal (V_out) and the voltage divider (R₁ and R₂). The voltage divider has the output signal on one end and ground (0 volts) on the other end. The feedback signal is that part of the output signal developed by R₁ (at point A). Another way to look at it is that the feedback signal is the amount of output signal left (at point A) after part of the output signal has been dropped by R₂. In either case, the feedback signal (V_fdbk) is the ratio of R₁ to the entire voltage divider (R₁ + R₂) multiplied by the output signal (V_out).

Mathematically, the relationship of the output signal, feedback signal, and voltage divider is:

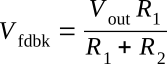
If you divide both sides of the equation by V_out:

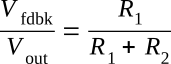
By inverting both sides of the equation:

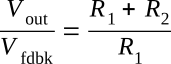
Separating the right-hand side:

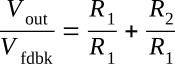
Remember:

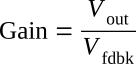
Therefore, by substitution:

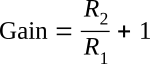
You can now see that the gain of the noninverting configuration is determined by the resistors. The formula is different from the one used for the inverting configuration, but the gain is still determined by the values of R₁ and R₂.