DC Circuits

Current Dividers

A current divider may be considered basically as some combination of impedances that will cause the output current of a network to be less than the input current. We shall restrict our discussion of current dividers to their simplest forms.

Consider figure below, which shows a line current I_t, feeding two branches so that I_t splits into I_R1 and I_R2. We should like to find a simple relationship between I_R2 and I_t in terms of the branch resistances R₁ and R₂.

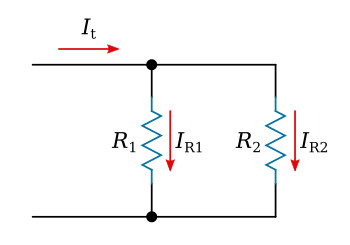
Since R₁ and R₂ are in parallel, the voltage across them must be the same. Therefore, I_R1R₁ = I_R2R₂. We want I_t and not I_R1 in our final expression. Therefore, let us express I_R1 in terms of I_t. Obviously, I_t = I_R1 + I_R2. Therefore, I_R1 = I_t - I_R2. By substitution, (I_t - I_R2)R₁ = I_R2R₂. Solving for I_R2, we obtain

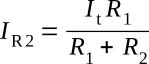
At this point, we want to show what a simple phrase such as "solving for I_R2" implies. The following algebraic manipulations were involved

Therefore

which as stated above yields

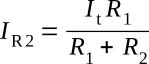
To continue with our problem, it can be shown similarly that

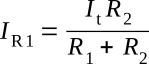
Notice here that, in this type of formula, as compared with that for the voltage divider, the numerator contains the shunt impedance, whose current we are not interested in.