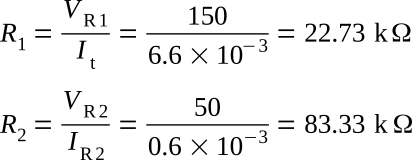DC Circuits

Voltage Dividers

Many electrical and electronics equipment use voltages of various levels throughout their circuitry. One circuit may require a 9-volt supply, another a 15-volt supply, and still another a 18-volt supply. These voltage requirements could be supplied by three individual power sources. This method is expensive and requires a considerable amount of room. The most common method of supplying these voltages is to use a single voltage source and a voltage divider.

A typical voltage divider consists of two or more resistors connected in series across a source voltage (V_in). The source voltage must be as high or higher than any voltage developed by the voltage divider. As the source voltage is dropped in successive steps through the series resistors, any desired portion of the source voltage may be "tapped off" to supply individual voltage requirements. The values of the series resistors used in the voltage divider are determined by the voltage and current requirements of the loads.

Consider the circuit of figure below, which represents a simple voltage divider. Physically we know that if V_in is applied to the input, the output V_R2 will be less than V_in because some of V_in is used up in forcing current through resistor R₁. The amount of voltage used up in R₁ is V_R1.

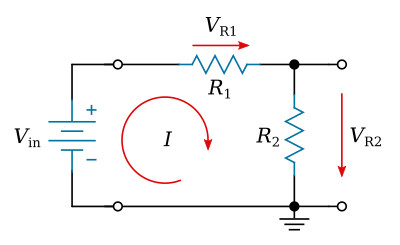
Likewise, the voltage appearing across R₂ is V_R2, the output voltage in this circuit. Now we should like to find a ready means of determining the voltage across R₂, which we are calling V_R2. (V_in, R₁ and R₂ are assumed known.)

By Ohm's law we know that the voltage across a specific resistor is equal to the current through that resistor multiplied by the ohmic value of the resistor. In equation form we would write V_R2 = I × R₂.

Apparently, to evaluate V_R2, we must first determine I. Recalling that I in the simple series circuit shown is

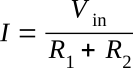
we can then substitute this value of I in the original expression for V_R2 — the first equation above — and obtain

The quantity R₂/(R₁+R₂) is then seen to be the ratio between the output and the input voltages.

If we were interested in the voltage across R₁, it would be equal to

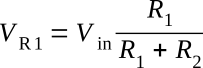
If a load resistance is placed across any of the resistors, voltage will be supplied to the load resistance and current will be drawn by it. When current is drawn from the divider, the total current flowing in the circuit will increase because the total resistance of the circuit has decreased.

If the total current flowing in the divider circuit is affected by the loads placed on it, then the voltage drops of each divider resistor will also be affected. When a voltage divider is being designed, the maximum current drawn by the loads will determine the value of the resistors that form the voltage divider. Normally, the resistance values chosen for the divider will permit a current equal to ten percent of the total current drawn by the external loads. This current which does not flow through any of the load devices is called bleeder current.

Example:
A simple voltage divider with no load applied is shown in the figure below.

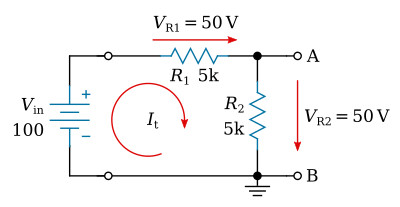
The voltage divider illustrated is composed of two resistors of equal value. Therefore, the voltage drop across each resistance will be the same. The total current flowing in the circuit will be

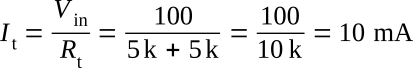
The potential difference between points (A) and (B) is equal to 50 V. If a resistor is placed between (A) and (B), the voltage drop between these points will be reduced.

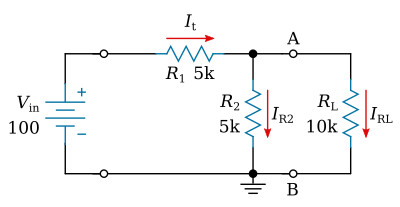
The figure above shows the same divider circuit with a load resistor connected. The total resistance may be computed

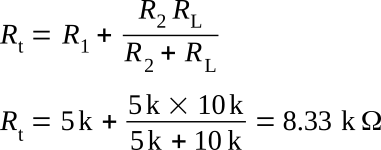
It can be seen that the total resistance has decreased. This results in a corresponding increase in current flow. Total current is determined as follows

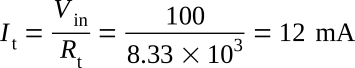
An analysis of the voltage drops shows the following change in the voltage distribution of the circuit

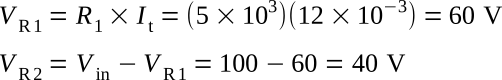
Notice that while the value of the voltage between points (A) and (B) is reduced the voltage drop across R₁ is increased. The amount of current flow through the load can be found in this manner

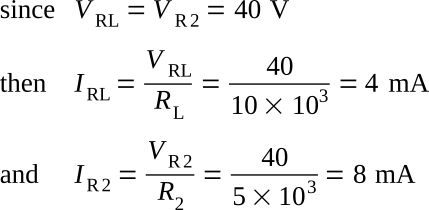
The variation of voltages and currents found in the previous example are undesirable in a voltage divider. It must be designed to provide voltages that are as stable as possible. A voltage divider consisting of two resistors will be designed using the circuit configuration shown in the figure below. The supply voltage is 200 V. It is desired to furnish a voltage of 50 V to the load drawing 6 mA.

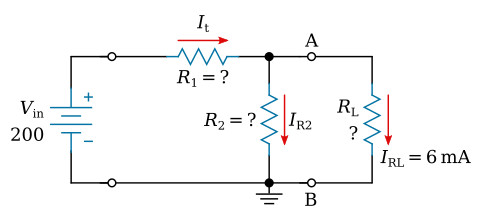
Assume bleeder current to be ten percent of the required load current.

Total load current (I_RL) is specified as 6 mA. The bleeder current through R₂, therefore should be

The bleeder current and the current through resistor R_L combine and both currents flow through R₁. This current value may be computed

The resistance value of R_L must be as follows

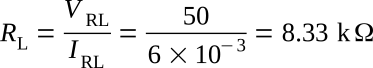
Computing for R₁ and R₂