DC Circuits

Power Transfer and Efficiency

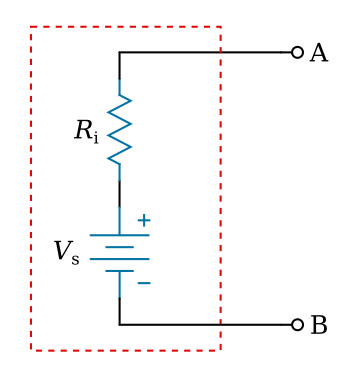
In any device that converts another form of energy to electric energy there is internal resistance. This is another way of saying that losses occur within the device so that not all its original energy is available at its terminals. In the figure below, points A and B represent the terminals of the battery. V_s represents the chemical energy converted to electric energy by the battery. If no current is drawn from the battery by an external load, the voltage across terminals A-B will be the V_s. V_s is also referred to as the no load voltage.

If a load is connected to terminals A-B of the figure above, current will flow, and there will be a voltage drop within the battery due to R_i. Thus the voltage at terminals A-B will be less than the no-load voltage by the amount of the voltage drop across R_i. This condition is shown in the figure below. As R_L is decreased the current drawn will increase, and as a result the internal voltage drop I×R_i will increase. As the internal voltage drop increases, the terminal voltage "seen" across the load decreases. This sequence of events shows that it is desirable that the internal resistance be very small to ensure that changes in terminal voltage will be negligible over a wide range of load currents.

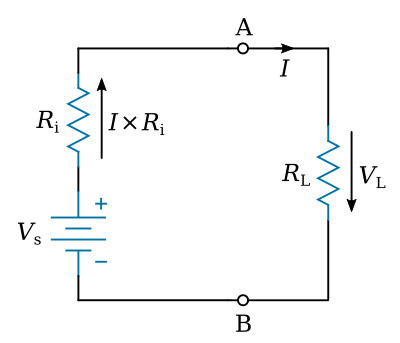
There is a relationship between load resistance and internal resistance of a source called the maximum power transfer theorem. The maximum power transfer theorem states:

Maximum power is delivered to a load when the load resistance equals the internal resistance of the source.

Whenever energy is converted from one form to another or transmitted, there are losses of energy as a result of this transmission. This situation gives rise to the concept of efficiency. Efficiency of power transfer is the ratio of power P_L received by a load to the power P_s supplied by a source of energy

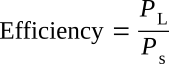
Efficiency has no units because it is simply a ratio of one quantity of power to another. Efficiency is normally specified as a percentage

The power transfer and efficiency is illustrated in the table and the graph of figure below. When the load resistance is 5 Ω, matching the source resistance, the maximum power of 500 W is developed in the load.

The efficiency approaches 100 percent as the load resistance approaches a relatively large value compared with that of the source, since less power is lost in the source. The efficiency of power transfer is only 50 percent at the maximum power transfer point (when the load resistance equals the internal resistance of the source). The efficiency of power transfer approaches zero efficiency when the load resistance is relatively small compared with the internal resistance of the source. This is also shown on the chart of figure above.

The problem of a desire for both high efficiency and maximum power transfer is resolved by a compromise between maximum power transfer and high efficiency. Where the amounts of power involved are large and the efficiency is important, the load resistance is made large relative to the source resistance so that the losses are kept small. In this case, the efficiency is high. Where the problem of matching a source to a load is important, as in communications circuits, a strong signal may be more important than a high percentage of efficiency. In such cases, the efficiency of power transfer should be only about 50 percent; however, the power transfer would be the maximum which the source is capable of supplying.