DC Circuits

Series-Parallel DC Circuits

In the preceding discussions, series and parallel DC circuits have been considered separately. However, there are circuits consisting of both series and parallel elements. A circuit of this type is referred to as a combination circuit. Solving for the quantities and elements in a combination circuit is simply a matter of applying the laws and rules discussed up to this point.

The basic technique used for solving DC combination-circuit problems is the use of equivalent circuits. To simplify a complex circuit to a simple circuit containing only one load, equivalent circuits are substituted (on paper) for the complex circuit they represent. To demonstrate the method used to solve combination circuit problems, the network shown in the figure below (view A) will be used to calculate various circuit quantities, such as resistance, current, voltage, and power.

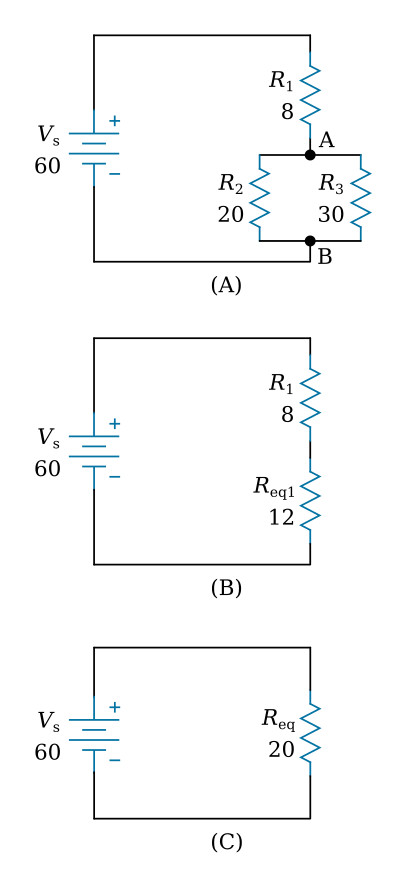
Examination of the circuit shows that the quantity that can be easily computed with the given information is the equivalent resistance of R₂ and R₃ (resistors in parallel).

Given: R₂ = 20 Ω, R₃ = 30 Ω

Solution:

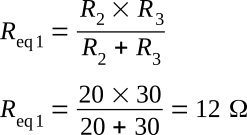
Now that the equivalent resistance for R₂ and R₃ has been calculated, the circuit can be redrawn as a series circuit as shown in the figure above (view B).

The equivalent resistance R_eq of this circuit (i.e. total resistance R_t) can now be calculated.

Given: R₁ = 8 Ω, R_eq1 = 12 Ω (resistors in series)

Solution:

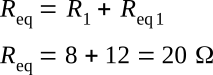
The original circuit can be redrawn with a single resistor that represents the equivalent resistance of the entire circuit as shown in the figure above (view C).

To find total current in the circuit:

Given: V_s = 60 V, R_t = 20 Ω

Solution:

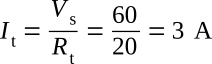
To find total power in the circuit:

Given: V_s = 60 V, I_t = 3 A;

Solution:

To find the voltage dropped across R₁, R₂, and R₃, refer to the figure above (view B). R_eq1 represents the parallel network of R₂ and R₃. Since the voltage across each branch of a parallel circuit is equal, the voltage across R_eq1 (V_eq1) will be equal to the voltage across R₂ (V_R2) and also equal to the voltage across R₃ (V_R3).

Given: I_t = 3 A, R₁ = 8 Ω, R_eq1 = 12 Ω (current through each part of a series circuit is equal to total current)

Solution:

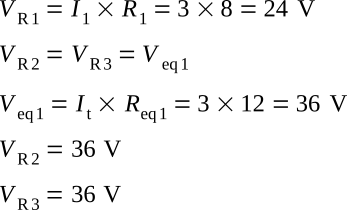
To find power used by R₁:

Given: V_R1 = 24 V, I_t = 3 A

Solution:

To find the current through R₂ and R₃, refer to the original circuit, figure above (view A). You know V_R2 and V_R3 from previous calculation.

Solution:

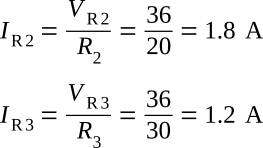
To find power used by R₂ and R₃, using values from previous calculations:

Now that you have solved for the unknown quantities in this circuit, you can apply what you have learned to any series, parallel, or combination circuit. It is important to remember to first look at the circuit and from observation make your determination of the type of circuit, what is known, and what you are looking for. A minute spent in this manner may save you many unnecessary calculations.

Having computed all the currents and voltages of the figure above, a complete description of the operation of the circuit can be made. The total current of 3 amps leaves the positive terminal of the battery and flows through the 8-ohm resistor (R₁). In so doing, a voltage drop of 24 V occurs across resistor R₁. At point A, this 3-ampere current divides into two currents. Of the total current, 1.8 amps flows through the 20-ohm resistor. The remaining current of 1.2 amps flows from point A, down through the 30-ohm resistor to point B. This current produces a voltage drop of 36 volts across the 30-ohm resistor. (Notice that the voltage drops across the 20- and 30-ohm resistors are the same.) The two branch currents of 1.8 and 1.2 amps combine at junction B and the total current of 3 amps flows back to the source. The action of the circuit has been completely described with the exception of power consumed, which could be described using the values previously computed.

It should be pointed out that the combination circuit is not difficult to solve. The key to its solution lies in knowing the order in which the steps of the solution must be accomplished.