AC Circuits

Inductance in AC Circuits

The Pure Inductance Circuit

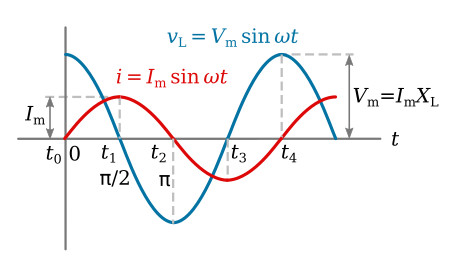
Inductance was defined as the property of a circuit to oppose change in current. This opposition results in induced EMF. The induced EMF is proportional to the rate at which current is changing as well as the magnitude of the inductance. This relationship can be given by the equation

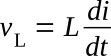
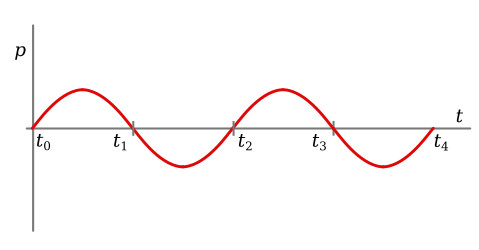
If a sinusoidal current is flowing in the inductance shown in the figure below, the induced voltage across the inductance can be plotted versus time.

The plot of current in the figure below increases from time t₀ to t₁. The current is increasing at a decreasing rate, and at time t₁ the instantaneous rate of change of current is zero. Therefore, v_L is zero at time t₁. From time t₁ to t₂ the current is decreasing; the rate of change of current is negative and v_L is negative. At time t₂, the rate of change of current is maximum, and thus v_L is maximum in the negative direction. At time t₃, the rate of change of current is zero, and thus v_L is again zero. From t₃ to t₄, the current is increasing, the rate of change is positive, and v_L is positive, reaching maximum at t₄, where the rate of change is maximum.

The maximum positive value of voltage occurs 90° ahead of the maximum positive value of current. The current is said to be lagging the voltage by 90 degrees. This phase relationship can be derived mathematically by applying the calculus.

From the previous equation, which is

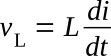
where

by differentiation, di/dt is found.

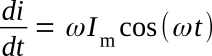
but

Therefore

By the general form of a periodic function (i.e. V_m sin (ωt + θ)),

and

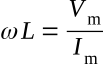
Since the ratio of volts to amperes is defined as opposition to current in ohms, the quantity ωL is measured in ohms. The quantity ωL is called the inductive reactance and is symbolized X_L

If V_m = 1.414 V and I_m = 1.414 I are substituted into the equation ωL = V_m / I_m, it is seen that the ratio of the effective values of voltage and current also equals the inductive reactance

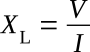
The reciprocal of inductive reactance is called inductive susceptance and is given the symbol B_L. The unit of inductive susceptance is the mho (or siemens S) when the frequency is in hertz and the inductance is in henrys.

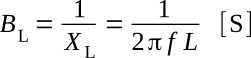
Example 1: An AC current with a frequency of 2 kHz and a maximum value of 0.15 A flows in a coil having 175 mH inductance. (1) Find the maximum voltage developed across the inductance. (2) Find the effective value of the voltage across the inductance. (3) Write the periodic functions representing the voltage and current.

Solution:

1.

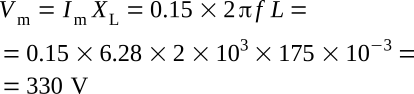
2.

The effective value of the voltage can also be found by first calculating the effective value of the current

Then

3. If the current is taken as the reference,

The voltage is leading the current in an inductive circuit

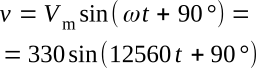
Example 2: A voltage across an inductance is 40 V when the current is 120 mA. The frequency of current and voltage is 400 Hz. Find the inductance.

Solution: The magnitude of the inductive reactance can be found

The inductance can now be calculated.

The power relationship in an inductive circuit can be analyzed by writing the equation for power with instantaneous values

Applying this equation to the figure above, we see that the instantaneous power is positive from t₀ to t₁, negative from t₁ to t₂, positive from t₂ to t₃, and negative from t₃ to t₄. The instantaneous power is plotted in the figure below. Positive power indicates that energy is taken from the source, and negative power that energy is returned to the source. Since over one complete cycle, from t₀ to t₄, as much energy is returned as is taken from the source, the net energy taken from the source is zero. Power over a complete cycle is therefore zero. This supports the definition that inductance is the property of a circuit to store energy in the form of a magnetic field. Thus, when current is increasing in magnitude, the magnetic field is building up and storing energy from the source. When current is decreasing in magnitude, the magnetic field is collapsing and returning energy to the source.

The net power is also given by the equation P = VI cos θ: