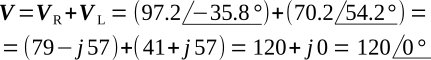Home Menu
Channel
Play
AC Circuits Alternating Voltages and Currents Resistance in AC Circuits Inductance in AC Circuits Capacitance in AC Circuits Complex Numbers in Electronics Impedance and Admittance Series RL Circuit Series RC Circuit Series RLC Resonant Circuit Parallel RL Circuit Parallel RC Circuit Parallel LC Resonant Circuit

Home   >   Textbooks   >   Basic Electronics   >   AC Circuits   >   Series RL Circuit   >  

AC Circuits

Series RL Circuit

On the basis of the discussion of impedance and the Ohm's-law equation, series AC circuits can now be investigated.

Resistance and inductive reactance
Resistance and inductive reactance.

Consider the circuit of figure above. The impedance Z of the circuit is the phasor sum of the inductive reactance and the resistance, since these components are in series:

Impedance of resistance and inductance 3

Applying Ohm's law,

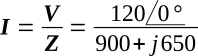
RL Ohm law

Converting 900 + j650 to polar form,

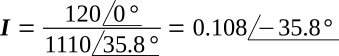
RL Ohm law 2

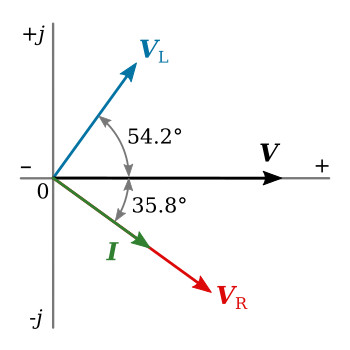
Since the circuit of figure above contains inductive reactance, it is to be expected that the current will lag the voltage. However, since the circuit is not pure inductance, the current will not lag by a full 90°. The current phasor was calculated and found to be lagging by 35.8°. The phase relationship between applied voltage V and current I is shown on the complex plane of figure below.

Phasors of figure above
Phasors of figure above.

In a series circuit, the sum of the phasors of the voltage drops must equal the applied voltage phasor.

For the series RL circuit,

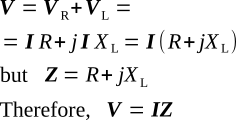
RL Ohm law 3

This is simply the algebraic transformation of the Ohm's-law equation. The value of VR and VL may now be calculated:

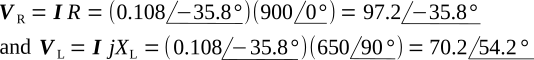
RL voltages

Plotting VR and VL on the complex plane of figure above shows that the voltage across the resistance is in phase with the current. The voltage across the inductance leads the current by 90°.

The phasor sum of VR and VL is given by

RL voltage


Previous Contents Next