Filters

Decibels

Decibel is a logarithmic expression used in filter applications as a unit of gain or loss. Characteristic of logarithmic operations, processes involving multiplication or division are reduced to additions or subtractions, that in many but not all cases is advantageous because the calculation is simpler. Decibels have come to be used in a manner that is not strictly correct according to the original definition; however, the massive use of the incorrect form on manufacturers' data sheets, in books, and throughout the electronics industry in general has virtually forced a redefinition of the term decibel.

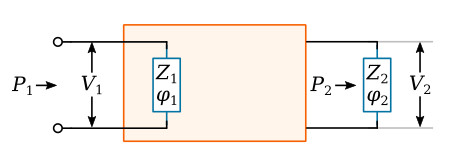
The original definition of decibels is embodied in the figure above. The box represents an amplifier, filter, or other device that may be passive or active. Input power P₁ across input impedance Z₁ with a phase angle φ₁ results in an input voltage V₁. Correspondingly, at the output there appears power P₂ in Z₂ (with a phase angle φ₂) along with V₂. The ratio of output power to input power of the circuit is

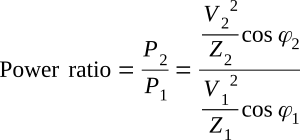
The power ratio computed by this equation has no units. The number of decibels denoting the power ratio is defined as

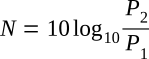
The power gain or loss in decibels (dB) is therefore found by taking the logarithm to the base 10 of the power ratio and multiplying it by 10. Combining the previous two equations gives

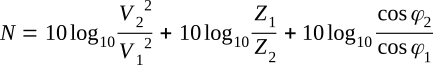
If the impedances are equal, the last two terms can be dropped. The remaining term can be manipulated to become

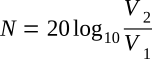
Note that this equation is an expression for the voltage gain or loss of the circuit expressed in dB. Strictly speaking, it should be used only when the input and output impedances are equal; for example, in a 600-ohm telephone system; however, this expression for voltage gain is used frequently even when the impedances are not equal. For simplicity, and because it is used extensively in literature, this equation is used to define voltage gain also in this textbook.

Example 1:
An amplifier has a voltage gain of 2; express this in dB.

Solution:

N = 20 log₁₀ 2 = 6.02 dB

Accordingly, an amplifier with a gain of 2 is usually said to have a gain of 6 dB.

Example 2:
A circuit attenuates an input voltage by a factor of 2; express its gain in dB.

Solution:

N = 20 log₁₀ 1/2 = -6.02 dB

Note that for a gain or loss of 2, the numerical answer is the same, namely 6 dB, but the gain is indicated by a plus sign while a loss or attenuation is indicated by a minus sign.

Example 3:
An amplifier has a 3-position gain switch to provide gains of 10, 1.0, and 0.1; express these gains in dB.

Solution:

Gain = 10: N = 20 log₁₀ 10 = 20 dB
Gain = 1: N = 20 log₁₀ 1 = 0 dB
Gain = 0.1: N = 20 log₁₀ 0.1 = -20 dB

The decibel is useful for representing large gains or losses. For example, to say that a voltage signal has increased 100 dB is much easier than to say the signal has increased 100,000 times. The value of using decibels in all cases to describe gain is highly questionable. For example, it is probably better to say that an amplifier has a gain of 100 than to state that its gain is 40 dB. Moreover, the use of dB to simplify cascaded-stage gain calculations can result in complication rather than simplification. This is illustrated by the following example:

Example 4:
Three amplifiers with gains of 3, 4, and 5 are connected in series. Express the overall gain as a number and in dB.

Solution:

Gain = 3×4×5 = 60
N = 9.5424 + 12.0412 + 13.9794 = 35.563 dB

In the above example, it is obvious that computations have not been simplified by adding dB's instead of multiplying gains, in fact, it is clear that expressing performance in decibels does not enhance comprehension of what the amplifier chain is doing in this case. Nevertheless, decibels will be used extensively in this textbook because they are widely used in filter design and because their use provides convenient graphs of filter performance.