Home > Textbooks > Basic Electronics > Filters > Types of Filters >
Filters
Types of Filters
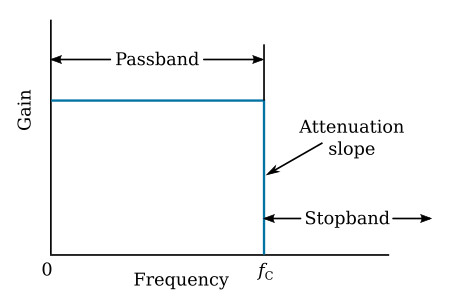
The design of any filter involves an attempt to achieve some unattainable ideal. For example, an ideal low-pass filter would have the amplitude response shown in the figure below, and would pass all frequencies with uniform gain in the pass region from DC to some cutoff frequency fc; above fc, in the stopband, all frequencies would be infinitely attenuated and the attenuation rate (slope of the curve at fc) would be infinite and would appear as a vertical straight line at fc.
Practical amplitude responses are not ideal; nevertheless, they are useful in many applications. Practical filters approach the ideal response in different ways; for example, some emphasize flatness in the passband, but do not have a particularly steep attenuation slope; others have steep attenuation slopes, but do not have flat gain in the passband. Certain classes of filters are designed to have linear phase response (important in minimizing overshoot or ringing in pulse circuits) at the expense of flatness of gain and steepness of attenuation. In general, a practical low-pass filter will approach the ideal by emphasizing one or more of the basic filter characteristics of passband flatness, attenuation slope, or phase linearity. Other factors, such as infinite attenuation of a particular frequency or the degree of attenuation in some given region of the stopband, are often important.
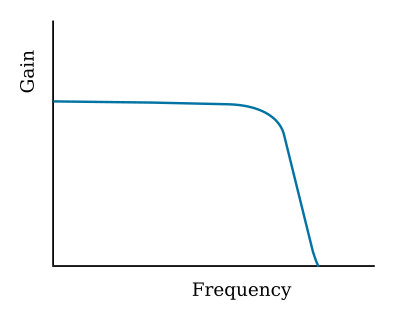
The various approximations to the ideal filter response are identified by such names as Butterworth, Chebyshev, Bessel, and others. Probably the most commonly used filter is the Butterworth, which has the characteristic amplitude response shown in the figure below. Butterworth filters have a maximally-flat response in the passband; that is, passband flatness is the ideal filter characteristic emphasized, but it is achieved at the expense of phase linearity and of steepness of attenuation slope. However, the attenuation slope of the Butterworth filter is quite good and, for applications where phase linearity is not important, the Butterworth response is an excellent general purpose approximation to the ideal filter.
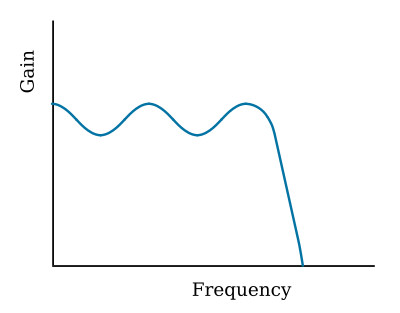
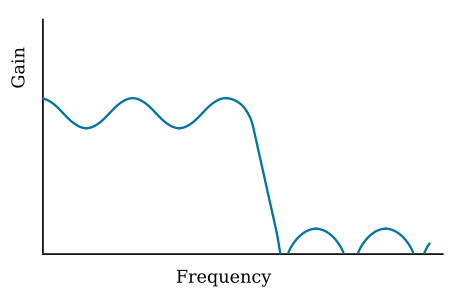
If steepness of attenuation slope, especially in the region of cutoff, is more important than passband flatness or phase linearity, the Chebyshev response, shown in the figure below is often applicable; however, there is ripple ("oscillation") in the passband. Chebyshev filters can be designed to provide different amounts of ripple, but the amplitude of the ripple in the passband remains constant for any given amount.
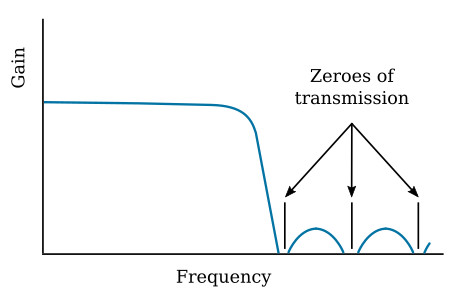
Both the Butterworth and the Chebyshev low-pass filters achieve infinite attenuation only at infinite frequency, but at any other frequency some signals will get through, even in the stopband. If infinite attenuation at particular frequencies in the stopband is required, the Inverse Chebyshev response shown in the figure below may be used; there is no ripple in the passband, but ripple does exist in the stopband and attenuation is infinite at certain frequencies.
A third filter in the Chebyshev family is the Complete Chebyshev; its response is shown in the figure below. The Complete Chebyshev is also called a Cauer, Elliptic-Integral, Elliptic-Function, or Zolatarev (but rarely Darlington, even though S. Darlington did much of the original work). The Chebyshev and Inverse Chebyshev filters are special cases of the more general class of Complete Chebyshevs. The Complete Chebyshev filter has ripple in the passband and stopband as well as infinite attenuation at certain finite frequencies.
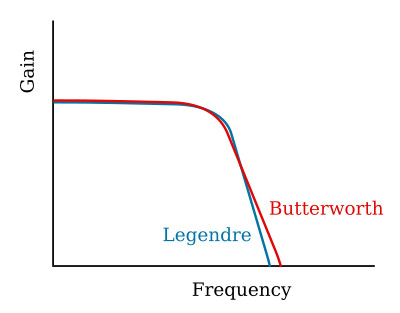
As has been emphasized, a Butterworth filter has a maximally-flat pass-band response and the Chebyshev family of filters provides a good attenuation slope. On some occasions the ripples of a Chebyshev filter are not tolerable and the attenuation slope of a Butterworth filter is inadequate. Designing a Chebyshev filter that will have a very small or zero ripple does not help because Chebyshev and Butterworth filters are of the same family, and a Chebyshev filter with zero ripple is a Butterworth filter. A solution in this instance would be to use a Legendre or Optimum filter. The amplitude response for such a filter is given in the figure below and, for purposes of comparison, the response of a Butterworth filter also is shown. Notice that the Legendre response is not as flat as that of the maximally-flat Butterworth response in the passband, but that the attenuation slope of the Legendre response is steeper. A key property of a Legendre filter is monotonicity; that is, for any value of gain there is a unique frequency. This is in contrast to the Chebyshev family in which a particular value of gain will occur at several frequencies because of ripple. Butterworth filters also are monotonic, but Legendre filters have the steepest possible cutoff for a filter which is monotonic.
Thus far filters have been discussed mainly in terms of their amplitude responses, which are plots of gain (or attenuation) versus frequency. However, these plots do not describe the complete transmission properties of a filter; for example, the phase characteristics of a network is one of the most important parameters of response for a filter designed for pulse work. When a rectangular pulse is passed through a Butterworth, Chebyshev, or Legendre filter, overshoot or ringing will appear on the pulse at the output. If this is undesirable, one of the members of the Gaussian family of filters can be used, the most common of which is usually called a Bessel filter. Bessel filters are sometimes called Thomson filters after the originator of the design method.
If ringing or overshoot must be avoided when pulses are filtered, the phase shift between the input and output of a filter must be a linear function of frequency; stated differently, the rate of change of phase with respect to frequency, or the group delay, must be constant. The net effect of a constant group delay in a filter is that all frequencies are delayed by the same amount; thus there is no dispersion of signals of different frequencies. Accordingly, since a pulse contains signals of different frequencies, its shape will be retained when filtered by a circuit that has a linear-phase response or constant group delay. Just as the Butterworth filter is the best approximation to the ideal of perfect flatness in a passband, so the Bessel filter is the best approximation to the ideal of perfect flatness or constancy of group delay in the passband because it has a maximally-flat group-delay response; however, this only applies to low-pass filters because high-pass and bandpass Bessel filters do not have the linear-phase property.
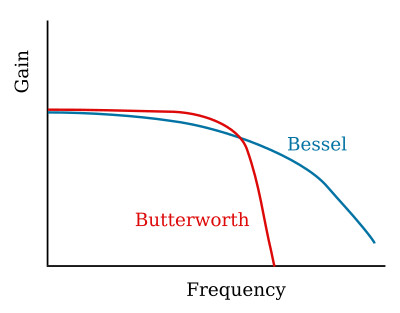
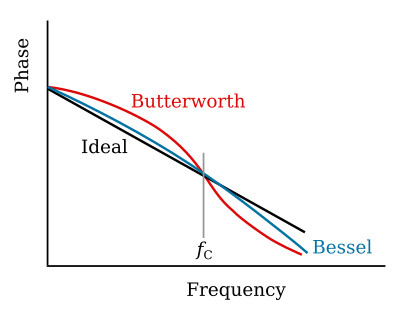
The figure above compares the amplitude response of a Bessel filter with a Butterworth. Note that the Bessel is a poorer approximation to the ideal both in flatness in the passband and in steepness of attenuation. The figure below compares the phase for an ideal filter, a Butterworth, and a Bessel. For an ideal filter, the group delay is constant at all frequencies and the phase shift is linear with frequency. The Butterworth filter group delay is not constant, and the plot of the phase angle versus frequency is nonlinear. In the passband region, the Bessel filter shows a reasonably linear phase-angle vs. frequency curve that is a fairly good approximation to constant group delay.
Transitional filters exist that have compromise characteristics that trade off the best properties of two types of filters; perhaps the most common is the Butterworth-Thomson filter that has characteristics lying between the maximally-flat amplitude of the Butterworth and the maximally-flat group delay of the Thomson filter (Bessel).
A summary of the main features of the types of filters discussed so far is given in the table below.
| Name of filter type | Main distinguishing characteristic | Remarks |
|---|---|---|
| Butterworth | Has maximally-flat amplitude response | The most popular general purpose filter |
| Chebyshev | Amplitude response has equal amplitude ripples in the passband | Attenuation slope is steeper than Butterworth near cutoff |
| Inverse Chebyshev | Amplitude response has equal amplitude ripples in the stopband | No passband ripple. Has zeros of transmission in the stopband |
| Complete Chebyshev | Amplitude response has equi-ripple in both pass- and stop-bands | Has zeros of transmission in the stopband |
| Legendre | Has no passband ripple, but has steeper attenuation slope than the Butterworth | Is not maximally flat |
| Bessel (also called Thomson) | Phase characteristic is nearly linear in the pass region, giving maximally-flat group delay | Good for pulse circuits because ringing and overshoot are minimized. Has poor attenuation slope |






